Physics-based Simulation of Extreme Wildfire Behavior on Sloping Terrain

Project Details

Student(s): Jad Samia
Advisor(s): Dr. Gilbert Accary
Department: Industrial & Mechanical
Academic Year(s): 2024-2025

Abstract

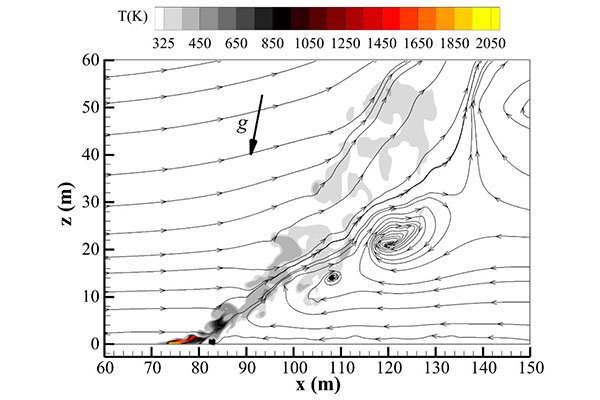
Wildfires pose a significant threat to ecosystems, human lives, and property, especially in regions characterized by variable topography. This work delves into the complexities of wildfire behavior on sloping terrain, where the combined effect of crosswind and slope acting in the same direction substantially influence fire behavior, rate of spread, and fire intensity. Fire regime depends on Byram’s convective number that was modified to account for slope effect according to Eq. 1 (Morvan and Accary 2024), where I is the fire intensity, g is Earth’s gravity, a is the slope angle, r and C_P are air respectively air density and specific heat at the ambient temperature T₀, R is the rate of fire spread and U_e is the effective wind speed that includes the component of buoyancy characteristic velocity acting in the direction of fire propagation. For steep slopes, this correction results in a convective number that is significantly different from the formulation proposed by Nelson (2015).

To test the effectiveness of the proposed Byram’s number expression, Large Eddy Simulations of shrubland fires were carried out using a 3D fully-physical CFD fire simulator (FireStar3D) under various terrain slopes and prevailing crosswind speeds, covering both wind-dominated fire regimes (N_C < 2) and plume-dominated ones (N_C > 10). Results show that the proposed modification of Byram’s convective number allows a better description of the obtained fire regime. In addition to the numerical simulations, a database consisting of 11 experimental fires carried out in shrublands was used to support the use of the new convective number formula. The heat transfer mechanisms governing fire propagation were described, highlighting in particular the role played by the convective cooling of unburnt vegetation in the case of a plume-dominated fire as the fire draws an adverse air flow in the opposite direction of fire propagation (see Fig. 1).

Fig. 1. Temperature field and streamlines obtained in the vertical median plane of a plume-dominated fire, 90 s after ignition, in the case of 10° slope, an initial crosswind speed of 0.5 m/s, and quasi-infinite fire front. Earth-gravity direction is indicated by an arrow.